1. 始めに

文部科学省は，「魅力ある大学院教育イニシアチィブ」として，国際的にも魅力ある大学院教育の展開を目標に，各大学から申請された取組みの中から特に優れた教育計画を選定し，これに対して財政支援を行うことによって，大学院教育の更なる展開（実質化）を図っています。10月25日には平成17年度「魅力ある大学院教育イニシアチィブ」の審査結果が公表され，私達が申請した「社会との関りを重視したMTS数理科学教育」（理工学研究科基礎理工学専攻数学系）が採択されました。

現代数学は，実社会のいろいろな所で，盛んに使われています。学問分野で言えば，理学や工学はもちろん，心理学や経済学・政治学などです。また，ファイナンスや医療業務などの現場で，数学が重要な役割を果たしていることは，良く知られています。私達のプログラム「社会との関りを重視したMTS数理科学教育」は，Multi-Truck-System数理科学教育を実現し，社会のいろいろな場所で，大学院で学んだ数学の力を生かしながら働く「新しいタイプの人材」，すなわち，社会と数学の間に「数理」という橋を架けることができる，そのような人材を育成することを目的とします。以下，もう少し詳しく説明しましょう。

2.明治大学における本事業の位置付け

このプログラムは，明治大学大学院教育改革の一環として，明治大学大学院研究科の指揮下に進められています。大学院理工学研究科基礎理工学専攻の中でも，比較的小規模の数学系を中心とする企画ですが，国内外大学院数理科学教育に新モデルを提供し，研究職だけではなく産業界・教育界への人材輩出にも寄与するなど，大学院教育改革の中でも先駆的地位を占めると評価されたからです。

3. 理工学研究科「I-MAST計画」との関係

明治大学理工学部・理工学研究科では，将来構想「I-MAST計画」の下に，国際的にも魅力ある大学院教育を実現し，国の競争力を強化し，悪循環「理工系離れ ⇒ 科学技術の軽視 ⇒ 産業の空洞化 ⇒ 技術立国の崩壊」に歯止めをかけるため，積極的方策を打ち出してきています。このプログラムも，I-MAST計画の一環として実施されるものです。

4. 「社会との関りを重視したMTS数理科学教育」の概要

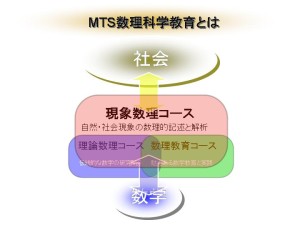
MTS（マルチトラックシステム）で下記3コースを開設し，研究者だけではなく，修士・博士の学位を持った高度専門職業人の養成を行います。

• 理論数理コース　代数学・幾何学・解析学という伝統的な「理論数学」の研究開発を目的とします。
• 現象数理コース　自然や社会現象の数理的理解と解析を目的とする新たな数学分野「現象数理学」の研究を行います。
• 数理教育コース　広い数理科学の知識と理解を持ち，数学の魅力を子供たちに伝えることができるような教員の養成を目指します。

数学は，経済学・ファイナンス・情報科学・工学・政治社会学などの学問分野においても，必須の役割を果たしています。国際競争力の強化には，豊かな数理科学リテラシーを持つ人材の養成が急務です。社会のニーズを理解し，様々な自然・社会現象に数理的記述を与えて，数学との間に架橋する力が要請されているのです。MTS3コースは，複線型骨太の履修形態で，この力を培うことを目標とします。本学グローバル・ビジネス研究科・政治経済学研究科・経営学研究科や企業・高等学校など学内外から招聘した講師による講義・セミナーを通し，広く数理科学に興味を持つ感受性を育みます。ジョブインターンシップを実施し，キャリアパスを開きます。

5. 「社会との関りを重視したMTS数理科学教育」の特色

上に述べたように，私達のマルチトラック（multi-truck）は，３つの柱よりなります。一番大きい柱は，現象数理コースです。基礎から積み上げた数学の知識を背景に，「数理科学的手法」を駆使して，自然や社会現象の解明に従事する，修士や博士の学位を持った「高度専門職業人」の養成を目的とします。残りの２つが，理論数理コースと数理教育コースです。

私達の計画の特色は，この３つのコースが有機的に組み合わさっていて，分離独立したものではないというところにあります。例えば，複数指導担当制の下に，受講学生達は主たる一つのコースの他に，もう一つのコースを副コースとして，履修あるいは聴講するよう求められます。現象数理コースの教育用セミナー「現象と数理」は，実社会の最先端専門家によるオムニバス形式のセミナーです。秋葉原サテライトキャンパスを通して，広く社会に公開される予定ですが，数学系のすべての前期課程学生に対し必修に指定されるなど，カリキュラム上の工夫がなされています。

 

理論数理コースは，代数学・幾何学・解析学という伝統的な学問分野で，研究者の養成を目的とします。

数理教育コースでは，ジョブインターンシップや現職の教員を助言者とするセミナーを開催します。子供たちに，数学の面白さを伝えるだけではなく，社会との関りの中で数学がいかに重要な役割を果たしているかを伝え，理解させることができる，そのような優れた教員の養成を目指します。

理工学部数学科では，毎年10名前後の学生が，学部を卒業して教職に就きますから，この大学院「数理教育コース」の充実は，少し長い時間スパンで見ると，大きな社会的意義があると考えられます。

6. プログラム実現のために

このプログラムに着手するため，私達は既に数年間に渡る周到な準備を重ねてきました。

 

1. 理工学部・理工学研究科の将来構想である「I-MAST」計画に則って，学部と大学院のカリキュラムを大改定し，「6年一貫教育」を実現しました。
2. 数理科学の3分野から，それぞれ世界的第一人者を招聘し，教育研究体制を強化しました。
3. 特定課題研究所「明治大学数理科学研究所」を設立しました。この研究所は数学系の全教員の他に，物理学系・情報科学系の教員と学外の研究者を加えて，約30名の所員により構成されています。数学系大学院の研究教育の基盤であって，このプログラムの実行拠点となります。
4. 本学グローバル・ビジネス研究科との連携を実現しました。カリキュラムとキャリアパスの双方に参加して頂きます。

7. 明治大学数理科学研究所について

数学系全教員の参加の下に，下記教育研究活動を行っています。

1. 「現象数理学」の創始
2. 「理工学研究科総合講義C」の開講
3. 「生田サロン」の開催
4. ４つの定期セミナーの継続実施

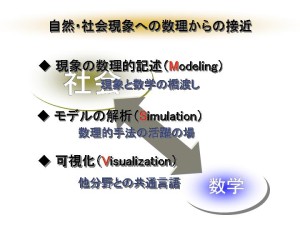
現象数理学は，新たな学問分野です。数学の基礎分野と理工学・生物学・社会学・経済学などとのインターフェースで，数理科学的手法を駆使し，現象の数理モデル構築・シミュレーション・可視化を目指します。「理工学研究科総合講義C」は，数理科学界の傑出した講師によるオムニバス形式の講義科目であり，全専攻学生を対象とします。「生田サロン」は，理工学研究科教員達の専攻の壁を越えた研究交流の場であり，大学院学生にも開放されています。数理科学研究所は，4分野（代数学・幾何学・数理解析学・現象数理学）で，様々な大学の研究者・大学院学生が参加した４種の定期セミナーを開催しています。

8.新しい教育システムの必然性 – なぜ今「MTS数理科学教育」なのか？

21世紀に入って，いろいろな分野で，膨大なデータが蓄積されてきています。生命とは何かというような問題を含めて，これらのデータに基づいて自然や社会現象を説明しようとするとき，数理科学の研究者は，まず最初に「モデル方程式」を導いて，現象と数学の間に橋渡しをします。これが一番大事で，難しい作業（モデリング，modeling）です。しかしながらこれに成功したとしても，モデル方程式というものは，普通は解けるものではありません。数学的には，解けないものが殆どです。そこで，計算機が登場します。最近の計算機はとても賢いですから，計算アルゴリズムを上手く開発すれば，その方程式の近似解を求めることができます。この近似解のことを現象のシミュレーション(simulation)といいます。最終段階がビジュアリゼーション(visualization)，すなわちCG等による可視化です。数学以外の分野との共通言語として，重要な役割を果たします。私達が数理科学的手法と言うとき，それは，モデリング・シミュレーション・ビジュアリゼーションという，この一連の操作MSVのことを意味します。

この作業には，現象をモデル化する能力，計算機を使いこなす能力の他に，基礎から積み上げた深い数学の知識が必要であることは，言うまでもありません。

さて問題は，実社会のいろいろな所で切実に要求されているにもかかわらず，我が国ではこのような作業MSVに熟練した人間がまだまだ少数であって，アメリカなど欧米諸国と比べるとかなり見劣りがする，ということにあります。そしてこのことが，我が国産業界の国際競争力低下の原因の一つになっていると，私達は考えています。人材を増やしこの事態に対処するには，小学校から大学院まで，これまで我が国で行われてきた数学教育では十分ではないのです。もっと社会と密接な関りを持った，新しい数学教育を構築する必要があります。

私達が実現しようとしているMTS数理科学教育は，そのような新しい数学教育のモデルの一つです。私達の組織は小さいものですが，この教育システムを然る可き規模で実施すれば，事態の改善に大きく寄与すると，私達は確信しています。「Math Everywhere」の旗印の下に，このプログラムの実現に向けて努力したいと考えます。

9.終わりに　-　私達の願い

21世紀に入り，コンピュータの発達や実験データの蓄積により，「生命とは何か」というような未解明の問題にまで，深い知見が得られるようになってきています。このような状況を数理の視点から眺めるとき痛感されることは，物事の本質を明らかにし，いざその構造を解明しようとする最終段階において，数理科学的方法の果たす役割の大きさです。社会のさらなる発展と人々の福祉のために，今こそ要求されることは，一人でも多くの人がこのような数理的解析の力を身につけることではないかと私達は考えています。自然と社会と人間に対する繊細で豊かな理解力を培うため，基礎から積み上げた広範で堅実な数理的知識を身につけようとすることも，社会人として，非常に大切な努力の一つなのです。

経済現象・生命現象・医学的問題等に数学的記述を与え，数学との間に橋を架けること，21世紀の数理科学はこのような「社会との関りinteraction」を通して発展するに違いありません。

我が数学系は，代数学・幾何学・解析学という伝統的な基礎部門のうえに，工学・生物学・経済学・社会学など諸分野のインターフェースで「現象の数理」とでも呼ぶべき，新たな学問分野を創造することを第一の目的としていますが，同時に，将来の数理科学を担う人材の育成も目指しています。大学院学生達は，数学系の営為に参加することにより，数学の知識をより確実に習得するだけではなく，モデリングやシミュレーション・ビジュアリゼーションなど，数学的知識が生きる数理科学の「現場」を豊富に体験することができます。数学系の願いは，彼らの前に研究の対象として限りなく大きな「数学・数理科学的世界」が開かれることだけではなく，学生達が社会にとってかけがえのない有為の人材となり，巣立って行くことにあるからです。本プログラムの基本コンセプト「社会との関りを重視した数理科学教育の構築」は，まさにここに原点を置くものです。